Disegnare una mesh 3D con C# in Unity
Non sarai mai capace di disegnare un tubo.
Così diceva la mia maestra di educazione artistica alle elementari. Vorrei trovarmela davanti oggi. Per dirle che in effetti aveva ragione.
Purtroppo però la vita mi ha messo davanti alla necessità di disegnare una serie di tubi per un progettino su Unity su cui sto perdendo numerose ore di sonno. L'idea è semplice: in questo giochino il giocatore può raccogliere e spostare oggetti, e io voglio che certi tipi di oggetti, una volta posati, vengano collegati automaticamente mediante tubi.

Ho provato a usare il componente "LineDrawer" di Unity, ma non mi ha soddisfatto: volevo poter customizzare questi tubi, e volevo che fossero solidi 3D, che reagissero all'illuminazione, che proiettassero ombre eccetera. Era dunque necessario creare delle vere e proprie mesh 3d per questi oggetti.
Problema: non è possibile disegnare queste mesh in Blender e importarle, come si fa normalmente con gli asset 3D. In primo luogo perché sono una capra con Blender, e secondariamente poiché questi oggetti devono essere creati in tempo reale a partire da posizioni iniziali e finali che non si possono stabilire a priori. Allora mi sono tuffato nella tana del coniglio e ho scoperto come si creano delle mesh programmaticamente.
Cosa è una mesh
Per prima cosa due parole su cosa è una mesh. Una mesh, nel contesto della modellazione 3d e semplificando molto, è la rappresentazione di un oggetto nello spazio 3D sotto forma di vertici e triangoli. I vertici sono identificati da coordinate spaziali (x, y, z). I triangoli, che vanno a formare le superfici dell'oggetto, sono costruiti semplicemente indicando la sequenza dei tre vertici sui quali sono costruiti.
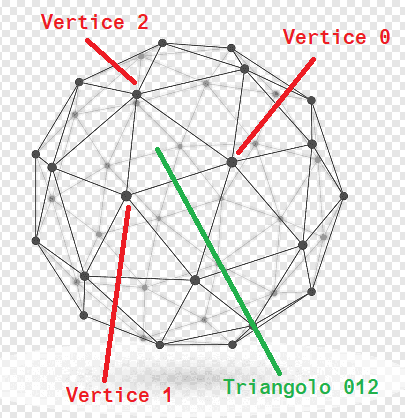
Se riusciamo a calcolare tutti questi numerini e darli in pasto a Unity, lui ci può costruire un oggetto tridimensionale.
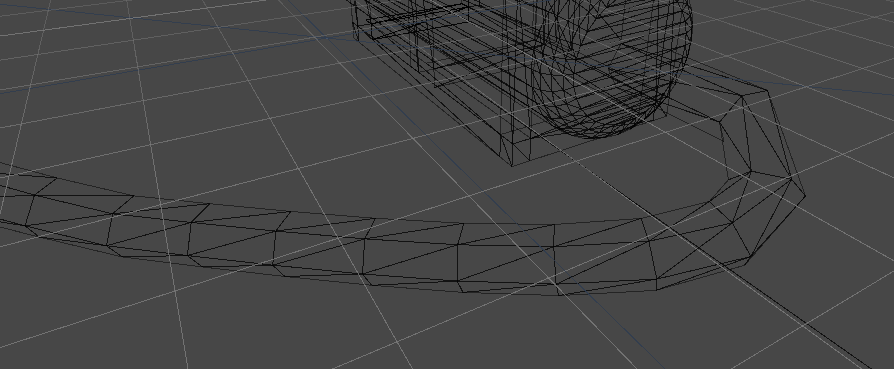
Capiamo un tubo
Il tubo avrà un punto di partenza e un punto di arrivo, nonché delle direzioni di partenza e arrivo impostabili (voglio che il tubo, indipendentemente dalla direzione generale, esca e entri negli oggetti collegati in direzione perpendicolare). Il tubo sarà diviso in un numero predefinito di segmenti. La sezione del tubo sarà un poligono regolare con un numero predefinito di lati.

Posizione delle "facce"
Il primo passo è individuare la posizione delle "facce". In questo contesto quando parlo di "faccia" intendo una sezione trasversale di tubo tra due segmenti, composta da N lati arrangiati attorno a un centro. Il tubo avrà un numero di "facce" pari al numero dei segmenti più uno. Il centro della prima faccia sarà ovviamente il punto di partenza del tubo, e il centro dell'ultima sarà il punto di arrivo.
Il centro della seconda faccia sarà calcolato a partire dal centro della prima faccia, spostandolo lungo la direzione di partenza (che deve essere garantita) di una distanza preimpostata. Secondo la stessa logica, anche la posizione della penultima faccia sarà calcolata a partire dalla posizione dell'ultima, spostandosi lungo la direzione di arrivo preimpostata. Per consentire la successiva smussatura degli angoli del tubo, ho seguito la stessa logica anche per la terza faccia e la terzultima. Il centro delle altre facce si calcola di volta in volta lungo l'asse tra la terza e la terzultima, dividendo la distanza in parti uguali.


Il codice per calcolare queste posizioni è più o meno qualcosa del genere. Facciamo abbondante uso delle funzioni vettoriali di C#, in particolar modo per somme/sottrazioni di vettori (Vector3).
Vector3[] faceOrigins = new Vector3[segments+1];
// La posizione della faccia zero e ultima sono impostate a priori
faceOrigins[0] = origin;
faceOrigins[segments] = end;
// Prime due facce (dopo l'origine)
faceOrigins[1] = faceOrigins[0] + (initialDir.normalized * initialSegmentLength);
faceOrigins[2] = faceOrigins[1] + (initialDir.normalized * initialSegmentLength);
// Ultime due facce (escludendo l'estremo)
faceOrigins[segments-1] = end - finalDir.normalized * finalSegmentLength;
faceOrigins[segments-2] = faceOrigins[segments-1] - finalDir.normalized * finalSegmentLength;
for (int i = 3; i < segments-2; i++){
Vector3 segmentStart = faceOrigins[i-1];
Vector3 distanceForSegment = (faceOrigins[segments-2] - segmentStart) / (segments-i-1);
faceOrigins[i] = faceOrigins[i-1] + distanceForSegment;
} Smussatura
Ora che abbiamo i punti centrali delle facce del tubo possiamo approfittarne per "smussare" un pò gli angoli. Al momento i due segmenti iniziali e finali sono in linea tra loro, come pure gli altri. Questo crea degli angoli molto forti e al tempo stesso delle sequenze di segmenti molto rigide, con un risultato poco realistico.

Possiamo applicare un meccanismo di filtraggio alle posizioni delle facce, per rendere il tubo più "tuboso":

Per ottenere questo risultato, possiamo applicare questo semplice ragionamento: per ogni tripletta di facce consecutive, calcoliamo la posizione della mediana tra la prima e la terza, e avviciniamo la faccia centrale a questa mediana. Possiamo poi ripetere questo filtraggio più volte per ottenere un risultato gradevole. Chiaramente la prima, ultima, seconda e penultima faccia non vengono spostate (così garantiamo che il primo e l'ultimo segmento del tubo restino nella direzione preimpostata).
Una cosa del genere:
if (enablePipeSmoothing){
for (int x = 0; x < pipeSmoothingSteps; x++){
for (int i = 2; i < faceOrigins.Length-2; i++){
Vector3 mediana = faceOrigins[i-1] + (faceOrigins[i+1] - faceOrigins[i-1])/2;
Vector3 distMediana = mediana - faceOrigins[i];
faceOrigins[i] = faceOrigins[i] + distMediana/2;
}
}
}Altezza del tubo
Un altro passaggio che possiamo fare con le posizioni delle "facce" del nostro tubo è il calcolo della posizione verticale. Al momento il nostro tubo è completamente rigido, senza flessione dovuta al suo presunto peso.

Per rendere il disegno più realistico io vorrei che questo tubo si appoggiasse al terreno.

La soluzione, banalmente, è che dobbiamo calcolare in corrispondenza di ciascuna faccia la collisione verticale con il terreno (ovvero la separazione dal layer terreno lungo l'asse verticale Y), e spostare la suddetta faccia in quella posizione (con uno spostamento verso l'alto pari al raggio del tubo).
Possiamo fare una cosa del genere:
// Calcola coordinata y facce per contatto terreno
// (sarà il mio Y minimo per ciascuna faccia)
float[] faceMinHeight = new float[faceOrigins.Length];
faceMinHeight[0] = originRelativePosition.y;
faceMinHeight[faceMinHeight.Length - 1] = endRelativePosition.y;
RaycastHit hit;
int layer_mask = LayerMask.GetMask("Terrain");
for (int i = 1; i < faceMinHeight.Length-1; i++){
if (Physics.Raycast(transform.position + faceOrigins[i], Vector3.down, out hit, layer_mask))
{
faceMinHeight[i] = (hit.point - transform.position).y + radius/2;
}
}
// Mette a terra tutti i segmenti
for (int i = 2; i < segments-1; i++){
faceOrigins[i].y = faceMinHeight[i];
}Smussatura altezza
Nel passaggio precedente abbiamo calcolato l'altezza minima per ciascuna faccia e abbiamo usato questa informazione per spostare ciascuna faccia a terra. Anche in questo caso, questi cambiamenti di direzione sono repentini e poco realistici.

Possiamo usare la stessa tecnica vista prima per applicare una ulteriore smussatura, stavolta solo sull'asse verticale (Y). Unico accorgimento: l'altezza di ciascuna faccia non può mai essere inferiore al valore minimo già calcolato.

Una cosa del genere:
if (enableHeightSmoothing){
for (int x = 0; x < heightSmoothingSteps; x++){
for (int i = 2; i < faceOrigins.Length-2; i++){
float diff = faceOrigins[i+1].y - faceOrigins[i-1].y;
faceOrigins[i].y = Math.Max(faceOrigins[i-1].y + diff/2, faceMinHeight[i]);
}
}
}Calcolo direzione delle facce
Ora che abbiamo tutti i punti di cui è composto il nostro tubo dobbiamo disegnare le "facce" vere e proprie. Prima, però, dobbiamo calcolare la direzione in cui sono orientate. Un sistema molto grezzo per ottenere questo risultato è calcolare la direzione di ciascuna faccia come parallela alla congiungente tra il centro della faccia precedente e della successiva.
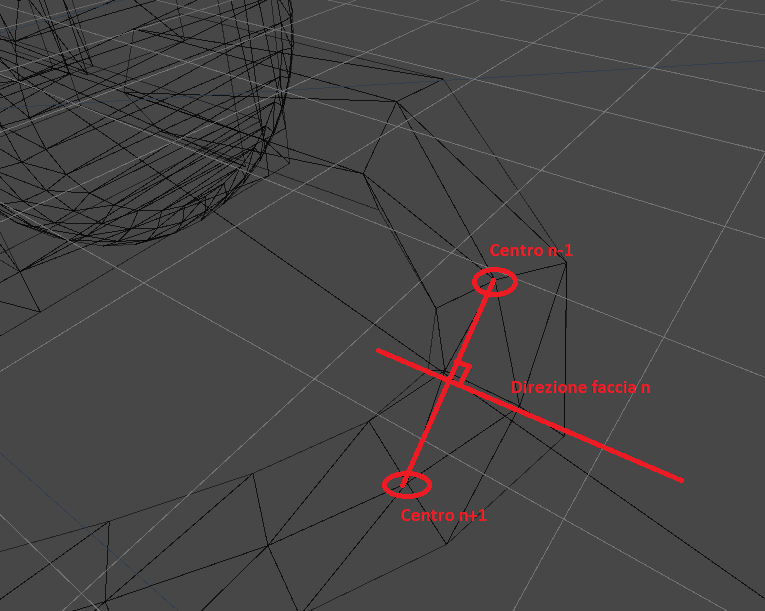
Il codice è qualcosa del genere:
Vector3[] faceDirections = new Vector3[segments+1];
for (int i = 0; i <= segments; i++){
// First face
if (i == 0){
faceDirections[i] = initialDir;
}
// Final face
else if (i == segments){
faceDirections[i] = (faceOrigins[i] - faceOrigins[i-1]).normalized;
}
// Other faces
else {
faceDirections[i] = (faceOrigins[i+1] - faceOrigins[i-1]).normalized;
}
}Calcolo vertici
A questo punto possiamo iniziare a fare sul serio, calcolando i vertici del tubo. Abbiamo la posizione di ciascuna faccia, la sua direzione, il numero di vertici e il raggio.
Per prima cosa dobbiamo trovare un vettore perpendicolare alla direzione del tubo. Sappiamo che in uno spazio 3D possiamo fare un prodotto vettoriale (cross) tra due vettori per ottenerne un terzo perpendicolare a entrambi. Scegliamo come secondo vettore il vettore verticale. Non è il sistema migliore (se il tubo non è esattamente parallelo al terreno ci possono essere delle deformazioni), ma il risultato è accettabile.
A questo punto abbiamo il vettore radiale, che possiamo normalizzare e scalare al raggio del tubo, e poi ruotare man mano attorno al vettore direzione (funzione Quaternion.angleAxis di Unity) per trovare i vertici.
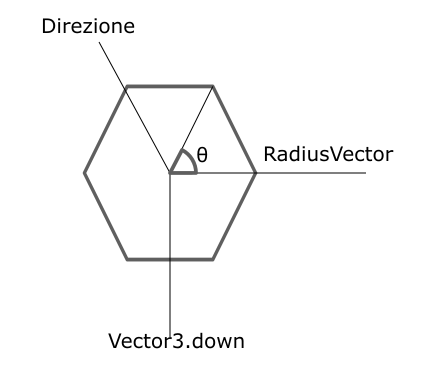
private Vector3[] _CreateFaceVertices(
int sides,
float radius,
Vector3 origin,
Vector3 dir
){
Vector3[] verts = new Vector3[sides];
float theta = 360 / sides;
Vector3 radiusVector = (Vector3.Cross(dir, Vector3.down).normalized * radius);
for (int i = 0; i < sides; i++){
float angle = theta * i;
verts[i] = origin + (Quaternion.AngleAxis(angle, dir) * radiusVector);
}
return verts;
} A questo punto abbiamo tutti i punti della nostra mesh, e li possiamo copiare sequenzialmente nel vettore finale dei vertici.
// One set of vertices for each face (i.e. segments +1).
Vector3[] verts = new Vector3[(segments+1)*sides];
for (int i = 0; i <= segments; i++){
Vector3[] segmVertices = _CreateFaceVertices(
sides,
radius,
faceOrigins[i],
faceDirections[i]
);
Array.Copy(segmVertices, 0, verts, i*sides, sides);
}Calcolo triangoli
L'ultimo passaggio che ci manca è la definizione dei triangoli, che costituiranno le superfici vere e proprie del nostro tubo. Definire i triangoli è semplice: dobbiamo solo indicare in sequenza, per ciascun triangolo, gli indici dei vertici che lo definiscono.
Ciascun segmento ha N superfici (con N numero dei vertici del tubo), che congiungono i rispettivi lati delle facce (ovvero, le rispettive coppie di vertici). Dobbiamo solo indicare due triangoli che coprano la superficie.
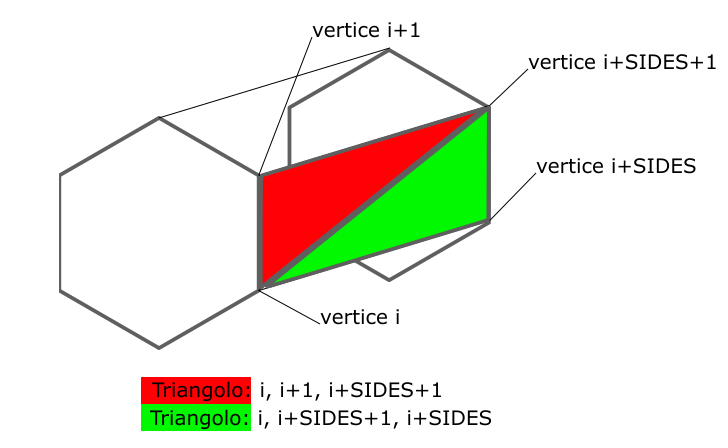
Con qualcosa del genere:
private int[] _BuildTris(int sides, int segments){
// One triangle set for each segment
// - each one composed by "sides" sides
// - each one composed by 2 tris
// - each one composed by 3 vertexes
int[] tris = new int[segments*2*3*sides];
int triPointsPerSeg = sides * 2 * 3;
int vertPerSeg = sides;
for (int s = 0; s < segments; s++){
int triPointOffset = triPointsPerSeg * s;
int vertOffset = vertPerSeg * s;
for (int i = 0; i < sides; i++){
// Primo tri
tris[triPointOffset + 6*i] = vertOffset + i;
tris[triPointOffset + 6*i+1] = vertOffset + i+1+sides;
tris[triPointOffset + 6*i+2] = vertOffset + i+sides;
// Secondo tri
tris[triPointOffset + 6*i+3] = vertOffset + i;
tris[triPointOffset + 6*i+4] = vertOffset + i+1;
tris[triPointOffset + 6*i+5] = vertOffset + i+1+sides;
if (i == sides-1){
tris[triPointOffset + 6*i] = vertOffset + i;
tris[triPointOffset + 6*i+1] = vertOffset + sides;
tris[triPointOffset + 6*i+2] = vertOffset + i+sides;
tris[triPointOffset + 6*i+3] = vertOffset + i;
tris[triPointOffset + 6*i+4] = vertOffset + 0;
tris[triPointOffset + 6*i+5] = vertOffset + sides;
}
}
}
return tris;
}Costruzione della mesh
Abbiamo tutti i componenti per creare la mesh, non ci resta altro da fare se non metterli insieme.
Mesh mesh = new Mesh();
mesh.vertices = verts;
mesh.triangles = tris;
mesh.RecalculateNormals();La funzione RecalculateNormals forza il ricalcolo automatico delle normali della mesh. L'argomento "normali" meriterebbe un post a sè, ma per ora ci accontientiamo di farle calcolare a Unity.
La mesh è pronta per essere utilizzata. Per mostrarla dobbiamo creare un Gameobject nella scena che abbia almeno un MeshRenderer (con associato un materiale) e un MeshFilter. Nel nostro script mettiamo in input un riferimento a questo oggetto, e inseriamo la mesh nel MeshFilter.
MeshFilter meshFilter = GetComponent<MeshFilter>();
meshFilter.mesh = mesh; Voilà, il gioco è fatto.
