Calcolare e disegnare un'orbita a partire dal vettore di stato con Javascript e ThreeJS - seconda parte
Come promesso nel precedente post, voglio descrivere sommariamente come si può calcolare un'orbita a partire da un vettore di stato e disegnarla con ThreeJS.
La spiegazione non sarà particolarmente discorsiva poichè è già stato detto tutto nel precedente post, ma ho pensato che potesse essere utile condividere il codice javascript che ho usato per mettere in pratica quanto detto in precedenza. Il codice è semplice e (decentemente) commentato.
La prima cosa da fare è definire una classe Vector che descriva un vettore, e che servirà a contenere tutte le informazioni geometriche. Inoltre in questa classe saranno implementate tutte le operazioni che riguardano i vettori: somme, scalature, prodotto scalare e prodotto vettoriale, modulo, normalizzazione. La classe avrà questo aspetto:
import * as THREE from '../build/three.module.js'
export default class Vector{
constructor(x = 0, y = 0, z = 0){
this.x = x;
this.y = y;
this.z = z;
}
static fromPolar(radius, inclination, argument){
return new Vector(
radius * Math.sin(inclination) * Math.cos(argument),
radius * Math.sin(inclination) * Math.cos(inclination),
radius * Math.cos(inclination)
)
}
/**
* Sums another vector to this. Returns a new Vector.
* @param {Vector} other Other vector.
* @returns {Vector} This.
*/
add(other){
return new Vector(
this.x + other.x,
this.y + other.y,
this.z + other.z
);
}
/**
* Returns a new Vector as difference between this and the
* other.
* @param {Vector} other Other vector.
* @returns {Vector} This.
*/
diff(other){
return new Vector(
this.x - other.x,
this.y - other.y,
this.z - other.z
);
}
/**
* Returns the length of this Vector.
*/
module(){
return Math.sqrt(this.x*this.x + this.y*this.y + this.z*this.z);
}
/**
* Normalize. Returns a new Vector with the same direction
* but unitary length.
*/
norm(){
const module = this.module();
return new Vector(
this.x / module,
this.y / module,
this.z / module
)
}
/**
* Returns a scaled version of this Vector.
* @param {number} value
*/
scale(value){
return new Vector(
this.x * value,
this.y * value,
this.z * value
)
}
/**
* Returns an inverted version of this Vector.
*/
minus(){
return new Vector(
-this.x,
-this.y,
-this.z
)
}
print(){
return({
x: this.x.toExponential(2),
y: this.y.toExponential(2),
z: this.z.toExponential(2),
module: this.module().toExponential(2)
})
}
/**
* Returns a copy of this Vector.
*/
clone(){
return new Vector(
this.x,
this.y,
this.z
)
}
/**
* Dot product of this Vector vs another.
* @param {Vector} other Other Vector
* @returns Dot product
*/
dot(other){
return (this.x*other.x + this.y*other.y + this.z*other.z)
}
/**
* Cross product of this Vector vs another.
* @param {Vector} other Other Vector
* @returns Cross product
*/
cross(other){
let x = this.y * other.z - this.z * other.y
let y = this.z * other.x - this.x * other.z
let z = this.x * other.y - this.y * other.x
return new Vector(x, y, z)
}
/**
* Angle between this and another Vector
* @param {Vector} other Other Vector.
* @returns Angle (rad)
*/
angle(other){
return Math.acos(this.dot(other) / (this.module() * other.module()))
}
/**
* Returns this vector as THREE.Vector3
* @returns
*/
toTHREEVector3(){
return new THREE.Vector3(
this.x,
this.y,
this.z
)
}
}Il passo successivo è costruire una classe destinata a contenere le informazioni relative a un singolo corpo celeste, in modo che siano raggruppate in maniera logica: positione, velocità, massa... Questa classe contiene anche i riferimenti alle mesh threejs che useremo per il disegno.
import Vector from './vector.js'
export default class Body{
constructor(name, mass, radius, SOIRadius){
// Nome del corpo celeste
this.name = name;
// Massa [Kg]
this.mass = mass;
// Raggio medio [m]
this.radius = radius;
// Raggio sfera influenza [m]
this.SOIRadius = SOIRadius;
// Posizione [m, m, m]
this.position = new Vector();
// Velocità [m^2, m^2, m^2]
this.velocity = new Vector();
this.mesh = null;
this.speedMesh = null;
this.lineMesh = null;
}
/**
* Calcola la posizione di un satellite.
* @param {*} height Altezza sopra la superficie [m]
* @param {*} inclination Inclinazione [°]
* @param {*} azimuth Azimuth [°]
* @returns
*/
calcSatellitePosition(height, inclination, azimuth){
let r = height + this.radius;
let theta = 2 * Math.PI * inclination / 360;
let phi = 2 * Math.PI * azimuth / 360;
let x = r * Math.cos(phi) * Math.sin(theta);
let y = r * Math.sin(phi) * Math.sin(theta);
let z = r * Math.cos(theta);
return this.position.add(new Vector(x, y, z));
}
clone(){
let newBody = new Body(this.name);
newBody.name = this.name;
newBody.mass = this.mass;
newBody.radius = this.radius;
newBody.SOIRadius = this.SOIRadius;
newBody.position = this.position.clone();
newBody.velocity = this.velocity.clone();
newBody.mesh = null;
return newBody;
}
}A questo punto dobbiamo creare un metodo che effettui tutti i calcoli. Non entro nel dettaglio dell'implementazione poichè segue passo passo le formule descritte nel precedente post.
/**
* Calculater orbital parameters of orbiting body.
* @param {Body} orbitingBody
* @param {Body} centreBody
* @returns
*/
export function orbitalCalcBody(orbitingBody, centreBody){
let velocity = orbitingBody.velocity
let position = orbitingBody.position
let attractorPosition = centreBody.position
// Constants
let M = centreBody.mass
// Initial state vector
let relPosition = position.diff(attractorPosition)
let v_0 = velocity.module()
let r_0 = relPosition.module()
let angle_0 = relPosition.angle(velocity)
// Specific energy (Earth orbit)
let specificEnergy = Math.pow(v_0, 2) / 2.0 - G * M / r_0
// Semimajor axis
let semiMajorAxis = - G * M / (2 * specificEnergy)
// Orbit eccentricity
let eccentricity = Math.sqrt(1+(
(2 * Math.pow(v_0, 2) * Math.pow(r_0, 2) * Math.pow(Math.sin(angle_0), 2) * specificEnergy)
/(Math.pow(G, 2) * Math.pow(M, 2))
))
// Orbit shape
let rApoapsis = (semiMajorAxis * (1 + eccentricity))
let rPeriapsis = (semiMajorAxis * (1 - eccentricity))
// Orbital period
let period = 2 * Math.PI * Math.sqrt(Math.pow(semiMajorAxis, 3) / (G * M))
// Specific angular moment vector
let h = relPosition.cross(velocity)
// Inclination
let inclination = Math.acos(h.y / h.module())
// Nodes vector
let n = new Vector(0, 1, 0).cross(h)
// Longitude of ascending node
let longAscNode = Math.acos(n.x / n.module())
if (n.z < 0) longAscNode = 2*Math.PI - longAscNode
if (isNaN(longAscNode)) longAscNode = 0
// Eccentricity vector
let eccVector = velocity
.cross(h)
.scale(1/(G*M))
.diff(relPosition.scale(1/relPosition.module()))
// Argument of periapsis
let argPeriapsis = Math.acos(n.dot(eccVector)/(n.module() * eccVector.module()))
if (eccVector.y < 0) argPeriapsis = 2*Math.PI - argPeriapsis
if (isNaN(argPeriapsis)) argPeriapsis = 0
// Velocità
let vApoapsis = Math.sqrt(G * M * ((2/rApoapsis)-(1/semiMajorAxis)))
let vPeriapsis = Math.sqrt(G * M * ((2/rPeriapsis)-(1/semiMajorAxis)))
// True anomaly
let trueAnomaly = Math.acos(eccVector.dot(relPosition) / (eccVector.module() * relPosition.module()))
if (relPosition.dot(velocity) < 0){
trueAnomaly = 2 * Math.PI - trueAnomaly
}
return({
v_0,
r_0,
angle_0,
specificEnergy,
eccentricity,
semiMajorAxis,
rApoapsis,
rPeriapsis,
period,
inclination,
argPeriapsis,
longAscNode,
vApoapsis,
vPeriapsis,
eccVector,
trueAnomaly,
orbitingBody,
centreBody
})
}Finalmente possiamo iniziare a disegnare qualcosa. Partiamo da un progetto ThreeJS (come ad esempio quanto descritto in questo post). Per prima cosa definiamo un metodo setMeshPosition, che ci servirà a posizionare le nostre mesh al punto giusto.
// Fattore di scala globale (la Terra misura 10 unità)
const scaleFactor = 10 / 6371000;
/**
* Set the position of the mesh.
* @param {Body} body Corpo da posizionare.
*/
export function setMeshPosition(body){
body.mesh.position.x = body.position.x * scaleFactor;
body.mesh.position.y = body.position.y * scaleFactor;
body.mesh.position.z = body.position.z * scaleFactor;
}Definiamo anche un metodo che ci servirà per inizializzare la mesh che useremo per disegnare l'orbita:
/**
* Inizializza la mesh lineare per disegnare la propagazione di una orbita.
* @param {*} scene
* @param {*} simSize Numero di step.
* @param {*} color Colore.
* @param {boolean} dashed
* @returns
*/
export function buildLineMesh(simSize, color = 'red', dashed = false){
// Create mesh with fake points, because the BufferGeometry has to be
// initialized with the right size.
const newSimPoints = []
for (let i = 0; i < simSize; i++){
newSimPoints.push(new THREE.Vector3(0,0,0));
}
const simGeometry = new THREE.BufferGeometry().setFromPoints(newSimPoints);
let simMaterial;
if(!dashed){
simMaterial = new THREE.LineBasicMaterial({
color : color
});
}
else {
simMaterial = new THREE.LineDashedMaterial({
linewidth: 1,
color: color,
dashSize: .5,
gapSize: .1
})
}
const mesh = new THREE.Line( simGeometry, simMaterial );
mesh.visible = false;
return mesh;
}Già che ci siamo, definiamo il metodo che riceverà i risultati dei nostri calcoli e li userà per piazzare la mesh lungo il percorso dell'orbita.
L'orbita viene disegnata a partire dal fuoco (la posizione del corpo attraente) dividendo l'angolo giro in ANGLESTEPS angoli e calcolando per ciascuno il raggio, usando la formula dell'ellisse. Non è il metodo ideale (l'angolo zero corrisponde al periapside, quindi le posizioni vicine a 180 gradi saranno più lontani tra loro e quindi l'ellisse risulterà meno fluida), ma per ora ci accontentiamo.
La mesh viene poi ruotata tre volte usando i valori di inclinazione, aegomento di periapside e longitudine del nodo ascendente.
export function orbitDraw(calcOrbit, orbitSim, angleSteps){
let eccentricity = calcOrbit.eccentricity
let semiMajorAxis = calcOrbit.semiMajorAxis
let inclination = calcOrbit.inclination
let argPeriapsis = calcOrbit.argPeriapsis
let longAscNode = calcOrbit.longAscNode
let eccVector = calcOrbit.eccVector
// Simulate orbit from parameters
for (let angleStep = 0; angleStep < angleSteps; angleStep++){
let theta = (angleStep * 360 / angleSteps) * Math.PI / 180;
// Ellisse
let r_theta = semiMajorAxis * (1 - Math.pow(eccentricity,2)) / (1 + eccentricity * Math.cos(theta))
let x = r_theta * Math.cos(theta) * scaleFactor;
let y = 0;
let z = r_theta * Math.sin(theta) * scaleFactor;
let posArray = orbitSim.geometry.getAttribute('position').array;
posArray[angleStep*3] = x;
posArray[angleStep*3+1] = y;
posArray[angleStep*3+2] = z;
}
orbitSim.geometry.setDrawRange(0, angleSteps)
orbitSim.geometry.attributes.position.needsUpdate = true;
orbitSim.visible = true;
orbitSim.computeLineDistances();
// Rotazione su parametri orbitali
// Reset rotation
orbitSim.rotation.x = 0
orbitSim.rotation.y = 0
orbitSim.rotation.z = 0
// Apply longitude of ascending node
orbitSim.rotateOnAxis(new THREE.Vector3(0,1,0).normalize(), -longAscNode)
// Apply argument of periapsis
let eccVectorPerp = calcOrbit.orbitingBody.position.diff(calcOrbit.centreBody.position).cross(calcOrbit.orbitingBody.velocity).norm()
orbitSim.rotateOnWorldAxis(eccVectorPerp.toTHREEVector3(), argPeriapsis)
// Apply inclination
orbitSim.rotateOnWorldAxis(eccVector.norm().toTHREEVector3(), inclination)
}Descriviamo la Terra:
var earth = new Body('Earth', 5.972e24, 6371e3, 0.929e9);
// Costruzione mesh
let earthGeometry = new THREE.SphereGeometry(
earth.radius * scaleFactor,
50,
50
);
let earthMaterial = new THREE.MeshPhongMaterial({
map: new THREE.ImageUtils.loadTexture("./images/2k_earth_daymap.jpg"),
color: 0xaaaaaa,
specular: 0x333333,
shininess: 5
});
earth.mesh = new THREE.Mesh(earthGeometry, earthMaterial);
scene.add(earth.mesh);
setMeshPosition(earth);..e il nostro satellite:
var ship = new Body('Ship', 100000, 200000, 0);
// Create ship mesh
var shipGeometry = new THREE.SphereGeometry(200000 * scaleFactor, 50, 50 );
var shipMaterial = new THREE.MeshPhongMaterial({
color: 'lightgreen',
transparent: true,
opacity: .8
});
ship.mesh = new THREE.Mesh(shipGeometry, shipMaterial);
scene.add(ship.mesh);
setMeshPosition(ship);
// Impostiamo posizione e velocità iniziali
ship.position: earth.calcSatellitePosition(400e3, 80, -40),
ship.velocity: new Vector(0, 1000, -7670-2500) Inizializziamo la mesh che useremo per disegnare l'orbita del satellite. Il numero di step definisce quanti punti saranno usati per disegnare la traiettoria.
let angleSteps = 36*2;
let orbitSim = buildLineMesh(angleSteps, 'yellow', true)
scene.add(orbitSim)A questo punto abbiamo tutti i tasselli, dobbiamo solo richiamare i metodi di calcolo e di disegno:
// Calcola e disegna orbita simulata
let calcOrbit = orbitalCalcBody(ship, earth)
orbitDraw(calcOrbit, orbitSim, angleSteps, scaleFactor)Voilà!
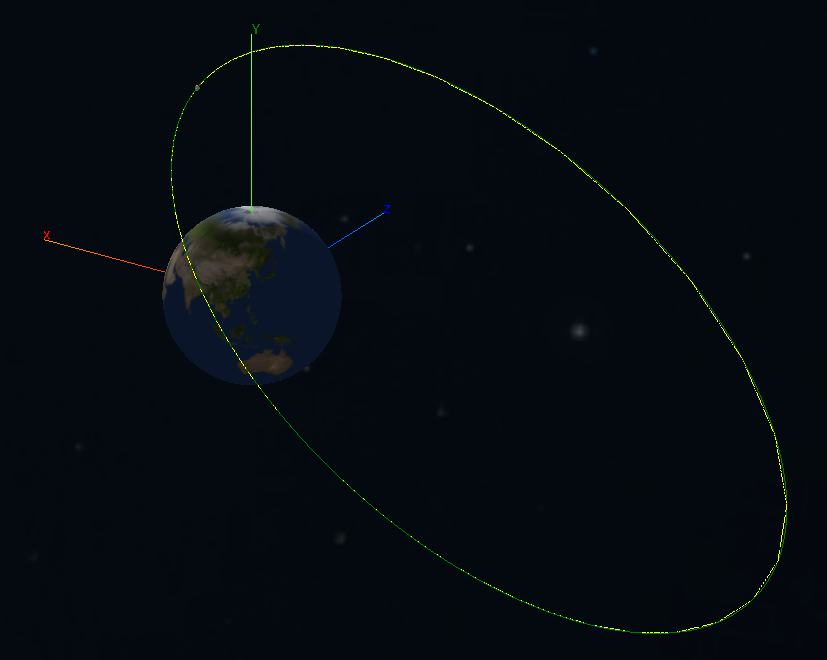
Alla prossima!
